The Natural Rate of Interest: Selected Conceptual Differences among Wicksell, Mises, and Woodford and Implications for Estimation and Monetary Policy

1. Background and Motivation

The natural rate of interest (NRI), represented by r*, is a ubiquitous latent variable in economics and finance. The concept of the NRI is attributed to Knut Wicksell (1936), who, concerned with the causes of changes in the value of money, first developed it in his 1898 book Geldzins und Güterpreise (Interest and Prices). Following disagreement with several scholars—in particular David Davidson (1909) and Ludwig von Mises—Wicksell (1934, 1935) modified the NRI concept to some extent in his two-volume Föreläsningar i nationalekonomi (Lectures on Political Economy), originally published in 1901 and 1906.^[1] Mises’s ideas on the concept of interest and more broadly on the macroeconomic dynamics of money and credit are in his 1912 Theorie des Geldes und der Umlaufsmittel (The Theory of Money and Credit) (Mises 1981) and his 1940 Nationalökonomie: Theorie des Handelns und Wirtschaftens, which he expanded into his 1949 Human Action: A Treatise on Economics (Mises 1998). The NRI was also at the center of significant discussions on the nature of the business cycle by Swedish economists Erik Lindahl (1939, 1958) and Gunnar Myrdal (1939) and regarding the value of money by Don Patinkin (1965). The NRI concept recently experienced a revival when, building on the real business cycle literature started by Finn Kydland and Edward Prescott (1982), it was integrated into modern macroeconomic theory by Michael Woodford (2003) in his book Interest and Prices: Foundations of a Theory of Monetary Policy.

Empirical estimates of the NRI abound. Recent estimates display a declining path over the last three to four decades. However, some stylized features of the data pose a challenge to available NRI estimates. First, despite this decline, the real return on productive capital remained relatively stable, and second, the assumed link between real interest rates and saving-investment determinants may well be unstable. This article aims to shed light on the possible causes of these two challenges to estimates of the NRI. While it agrees with scholars who argue that Woodford’s reformulation of Wicksell’s NRI is incompatible with Wicksell’s views, this study goes further and argues that, in contrast to Wicksell’s views, both Mises’s view of the interdependence between the financial market interest rate and the NRI and his business cycle theory can help in understanding the challenges faced by estimates of the NRI. The estimation of a time-varying parameter factor-augmented vector autoregressive (FAVAR) model over the 1980–2020 sample period, when the link between interest rates and saving-investment determinants seems stable, suggests that US monetary policy may have had a persistent downward influence on real interest rates, increasing its gap with the real return on productive capital. The estimates also provide evidence supporting some key features of Mises’s business cycle theory.

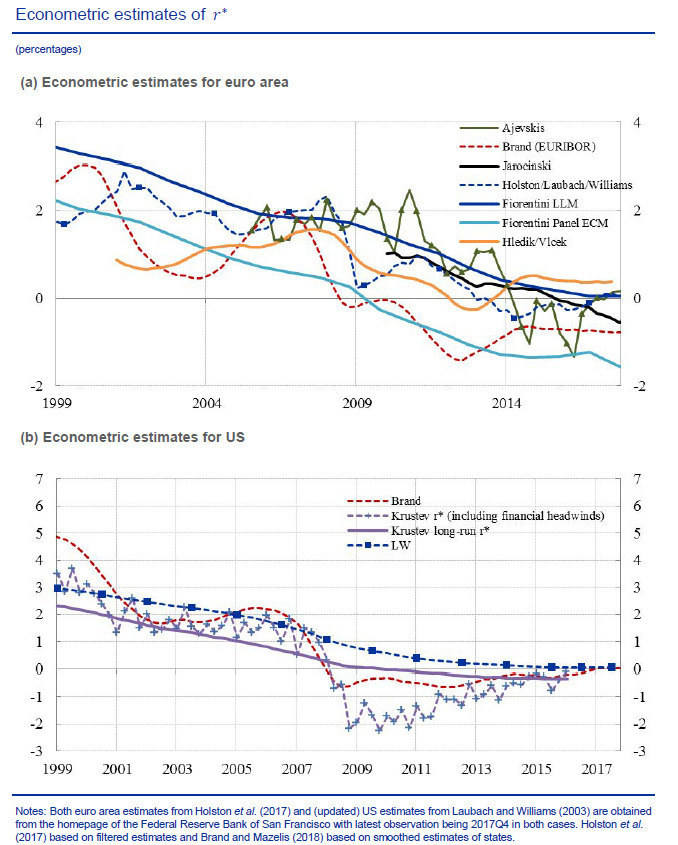
The declining trend in the NRI, sometimes even including negative values, appears when researchers use models of closed and open economies, either semistructural or dynamic stochastic general equilibrium (DSGE) models. Figure 1, taken from Brand, Bielecki, and Penalver (2018, 25), summarizes a set of estimates from a wide variety of semistructural models of the NRI for the euro area and the US from 1999 to 2018.^[2] These are the semistructural approaches of Holston, Laubach, and Williams (2017), Hlédik and Vlček (2018), Krustev (2018); and Brand and Mazelis (2019); the macrofinance model by Ajevskis (2018); the panel error-correction model by Fiorentini et al. (2018); and the rolling Bayesian vector autoregression (BVAR) by Jarocinski (2017).^[3] Estimates for the euro area and the US show a decline which accelerated after the 2007–8 global financial crisis (GFC). Most estimates show a negative NRI since then.

Figure 1.Estimates of the euro area and US NRI using semistructural models

Source: Brand, Bielecki, and Penalver (2018, 25).

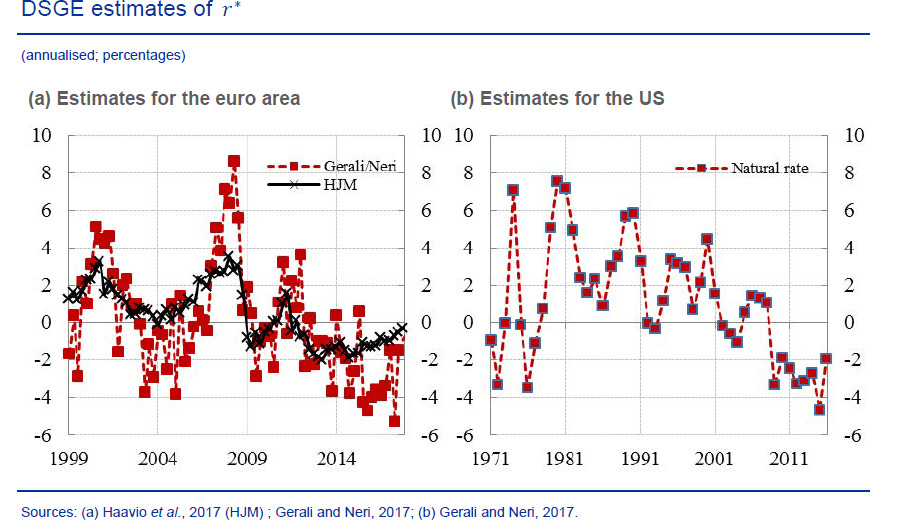
Figure 2 displays euro area and US estimates using DSGE models from the same study. These models follow Woodford’s (2003) definition of the NRI as the real interest rate that would prevail in a counterfactual economy characterized by flexible prices and wages in the absence of shocks to markups on goods and labor markets. The models are by Haavio, Juillard, and Matheron (2017) and Neri and Gerali (2019), who follow the approach of Smets and Wouters (2007) and add financial frictions. Estimates again display a declining NRI but are more volatile and contain more frequent periods of a negative NRI than several semistructural models.

Figure 2.Estimates of the euro area and US NRI using DSGE models

Source: Brand, Bielecki, and Penalver (2018, 33).

Both DSGE models identify a “risk premium shock” as the main driver of the fall in the NRI. Presumably, this shock modified households’ effective discount rate for one-period risk-free bonds and, according to Fisher (2015), can be interpreted as a shock to demand for safe and liquid assets. In Neri and Gerali (2019), the decline in the NRI is also attributed to a shock to the marginal efficiency of investment, capturing (unidentified) disturbances in financial intermediation. Other explanations for the decline in the NRI vary across studies. These include lower trend growth (e.g., Garnier and Wilhelmsen 2005); demographic factors, such as population aging and life expectancy (e.g., Carvalho, Ferrero, and Nechio 2016); rapid, unanticipated globalization and its depressing effects on markups (e.g., Natal and Stoffels 2007); and financial conditions (e.g., credit-supply and funding conditions), notably after the GFC (e.g., Borio 2014).

It is widely acknowledged that empirical estimates of the NRI are model dependent, and model estimates display high statistical uncertainty. These features naturally translate into uncertainty in the assessment of monetary conditions and are obvious in the estimates from the state-of-the-art modeling and technical capabilities displayed in figures 1 and 2.^[4]

Several stylized features pose a challenge for available NRI estimates. The following two are fundamental: (1) the difficulty of identifying “the” relevant real rate of interest and (2) the poor match between the time-series properties of the traditional determinants of real interest rates and savings and investment. The first challenge stems from the observation that, in contrast to the estimated decline in the NRI, estimates of the return on physical capital have remained almost constant, indicating a persistent decoupling between financial markets’ returns and the real economy. Figure 3, from Caballero, Farhi, and Gourinchas (2017)—a widely cited paper—shows the discrepancy between low real yields on US treasuries and the real return on physical capital. The authors use a simple growth and production model to reconcile these differences. They argue that rising markups and surging premia on “capital risk”—defined as the expected return on physical capital in excess of the risk-free rate—largely explain the discrepancy between the real yields on US treasuries and the real return on physical capital.^[5]

Figure 3.Real yields on US Treasury bills and return on physical capital

Source: Caballero, Farhi, and Gourinchas (2017, 615).

The second challenge to available estimates of the NRI is illustrated by Borio, Disyatat, and Rungcharoenkitkul (2017), who use a sample of nineteen economies over a period going back to 1870 to show that real interest rates are not driven by variations in desired savings and investment, but rather by variations in real yields, which seemingly reflect differences in monetary policy regimes.^[6] Controlling for the widely accepted determinants of desired savings and investment (e.g., demographics, potential growth, dependency ratio), they find only life expectancy to be statistically significant and only in the post-Volcker period. These findings (see also Borio, Disyatat, and Rungcharoenkitkul 2019 for an econometric analysis) challenge the theoretical foundations of most models used for the empirical estimation of the NRI. In fact, Brand, Bielecki, and Penalver (2018, 8) European Central Bank Occasional Paper “The Natural Rate of Interest: Estimates, Drivers, and Challenges to Monetary Policy” states: “This negative relationship between consumption and real interest rates underpins all models covered in this report.”

One logical implication advanced by Borio, Disyatat, and Rungcharoenkitkul (2019) is that monetary policy may itself be a driver of the NRI. This possibility is of particular significance not just historically, but for current monetary theory and policy. A look at the data for the US returns on assets is appropriate. Data from Jordà, Schularick, and Taylor (2017); Chen et al. (2022); and Jordà et al. (2019) show that between 1980 and 2008 total returns on equity in the US were on average 1.7 percentage points higher than the return on US government bonds. As shown in table 1, this difference increased to over 9 percentage points in the post-GFC period (2009–20). This increase in the equity risk premium^[7] broadly mimics the difference in total returns between risky assets and safe assets (i.e., a rise from 2.2 percent over 1980–2008 to 8.0 percent in the post-GFC period). The increase in equity returns mostly reflects an increase in capital gains, which more than offset the much smaller decline in dividend returns. The US stock market may have benefitted from the long period of accommodative monetary policy.^[8] Returns on safe assets more than halved, with unconventional monetary policy contributing to a decline in bond rates from 7.4 percent to only 2.4 percent. Average capital gains dropped from 3.3 percent to 2.4 percent.

The rest of this article is organized as follows. Section 2 first discusses three areas where the literature has argued that Woodford’s interpretation of Wicksell may be inaccurate. These areas are the concept of the NRI, Wicksell’s “cumulative process”—which could be referred to today as the dynamics of inflation—and money neutrality.^[9] This third part of section 2 goes on to address the differences between Wicksell and Mises regarding the interdependence of the loan rate of interest and the NRI, and the corresponding relation between the money market and the real economy. These differences matter because they led Mises to study the issue of capital accumulation and develop his theory of the business cycle. Based on the discussion in section 2, section 3 computes the rate of return on capital for the US to offer an alternative to Caballero, Farhi, and Gourinchas’s (2017) explanation of the gap between real yields on securities and the real return on physical capital. Section 4 provides an econometric analysis of the domestic and international effects of US monetary policy shocks, providing evidence that monetary policy may explain in part the gap between real yields on securities and the real return on physical capital. Section 5 provides concluding remarks and implications.

2. Wicksell, Mises, and Woodford—Selected Differences

Differences between Woodford and Wicksell have been discussed extensively in the literature (e.g., Amato 2005; Boianovsky 2006; Laidler 2006; Trautwein 2011; De Fiore and Tristani 2011). Differences between Wicksell and Mises have been addressed less frequently (e.g., Dempsey 1943; Del Vecchio 1917; Bellofiore 1998; Festré 2006). This section brings together these strands of literature to address three key areas relevant to the dominant interpretation of the NRI and its empirical estimates: Wicksell’s and Woodford’s concepts of the NRI; (2) Wicksell’s cumulative process and his disagreement with Mises on the interdependence between the financial market interest rate and the NRI; (3) long-run money neutrality in Wicksell’s static analysis, Woodford’s model, and Mises’s business cycle.

2.1. The Concept of the NRI: What Are the Differences between Wicksell and Woodford?

2.1.1. Wicksell’s Concepts of the NRI

Wicksell used at least three somewhat different concepts of the NRI in his writings. While he criticized Eugen von Böhm-Bawerk’s theory of capital, his widely referenced definition of the NRI in Interest and Prices clearly acknowledges the Austrian school’s view that more roundabout methods of production imply a higher marginal productivity of capital. According to Wicksell (1936, 102), “There is a certain rate of interest on loans which is neutral in respect to commodity prices, and tends neither to raise nor to lower them. This is necessarily the same as the rate of interest which would be determined by supply and demand if no use were made of money and all lending were effected in the form of real capital goods. It comes to much the same thing to describe it as the current value of the natural rate of interest on capital.” Therefore, the NRI is the rate of interest which would be determined by supply and demand if no use were made of money and all lending were effected in the form of real capital goods, or savings in natura. This definition of NRI equates the monetary (or bank loan) rate determined by the financial sector with the rate in the capital market at which the supply of and demand for real capital goods are in equilibrium.^[10] Wicksell emphasizes in this definition the role of the NRI in equating savings and investment and bringing about macroeconomic price stability.

A second Wicksellian definition of the NRI is found in his Lectures on Political Economy, where he refers to the NRI as the “normal rate”: “The rate of interest at which the demand for loan capital and the supply of savings exactly agree, and which more or less corresponds to the expected yield on the newly created capital, will then be the normal or natural real rate” (Wicksell 1935, 192–93). For Wicksell (1936, 226n), in an efficiently functioning banking system, savings always have a corresponding real equivalent which first takes the form of additions to the stock of raw materials and consumption goods, which later become what he calls “mobile” or “free” capital." This free and mobile capital is necessary as means for sustaining those who furnish the labor and land during the time required for the production of fixed real capital (i.e., the waiting period). Wicksell’s second concept of NRI puts the Austrian notion of the time structure of capital clearly at the center of his “pure credit” economy model of price level determination. Capital has not only a value dimension in monetary terms in each time period, but also a time dimension represented by the time that elapses between the application of labor and land and the emergence of the consumption goods that they are expected to generate. This concept of capital was later to become a key part of the Austrian tradition represented by Mises and Friedrich von Hayek, and it was also at the heart of the Cambridge capital controversy of the 1950s and 1960s.^[11]

Wicksell’s third definition of the NRI can be found in the exposition of his well-known cumulative process in chapter 9 of Interest and Prices, where he writes, “It has now to be supposed that, for some reason or other, a difference arises between the natural rate of interest and the contractual rate of interest. . . . Suppose that the natural rate is raised to i +1 per cent., while the banks maintain their customary rate of discount i. To whose advantage will this difference accrue? In the first place, of course, it accrues to the entrepreneurs” (Wicksell 1936, 141). According to this definition, the NRI is largely equal to the real profit rate (Festré 2006). For Wicksell, under perfect competition, equilibrium in both the real capital market and the loan market requires a new NRI that is common across different roundabout production processes.

Despite Wicksell’s somewhat different definitions of the NRI, there is one common empirical feature, and the three definitions share three common conceptual features. From an empirical viewpoint, Wicksell never assumed that the NRI is directly observable, as it is a conceptual point of reference—an equilibrium—rather than a measurable parameter.^[12] From a conceptual viewpoint, first, the NRI is always characterized by being consistent with equilibrium between savings in natura and investment. Second, this equilibrium is a long-run concept, and the NRI is itself subject to variations because of exogenous forces, such as technological shocks or changes in the labor force (Amato 2005). In contrast, the market rate of interest is a contractual rate. Third, the price level (or the inflation rate) is for Wicksell a measure of the investment-savings imbalance.^[13]

2.1.2. Woodford’s Concept of the NRI

Woodford (2003, 248) defines the NRI “as the equilibrium real rate of return in the case of flexible prices.” In chapter 5, he relates the NRI to the natural rate of output: “Indeed, the natural rate of interest is just the real rate of interest required to keep aggregate demand equal at all times to the natural rate of output” (Woodford 2003, 248). This NRI is therefore a real interest rate consistent with output at its potential level and with inflation at its target. For Woodford, the NRI is a function of the representative agent’s discount rate and stochastic shocks when labor is the only factor of production. If capital is added to the production function, the NRI is a function also of the level of the capital stock (e.g., Gertler, Gilchrist, and Natalucci 2007). Further, in an open economy, the NRI depends on foreign output shocks as well (e.g., Galí and Monacelli 2008). What underlies all these models—henceforth “Woodford-style” models for simplicity—is the classical dichotomy by which the economy’s real equilibrium can be determined independently of the nominal equilibrium. The NRI can be pinned down without reference to nominal variables, in particular without reference to a payment system that is essentially different from an accounting system of exchange—that is, a nonmonetary model.^[14] This system of exchange is a perfect barter system (McCallum 2003).

Therefore, Woodford-style models exhibit the Hahn property, which “arises when in non-monetary models, accounting systems of exchange based on a Walrasian or Arrow-Debreu auction, have attached them some or all of the characteristics of money, credit and debt” (Rogers 2006, 295). Frank Hahn (1973) calls these types of models “inessential sequence economies” because while money can always be added to them, they imply a complete theoretical equivalence between monetary and nonmonetary equilibria. Barter is treated as if the double coincidence of wants, the dimensionality curse of millions of relative prices, and the settling of debt in complex modern economies have been somehow solved. As a result, when these models add money as a friction (as cash in advance or cash in arrears) that monetary policy will eliminate, it is logically unavoidable, albeit counterintuitive, that money is welfare-reducing because it imposes a constraint on the equilibrium solution generated by the Walrasian auction.

In contrast, in Wicksell’s pure credit economy the money supply is made up of current account balances. Money is endogenous, and the classical dichotomy between money and goods markets does not hold. In the loan market, firms borrow funds to invest, and households lend their savings in a process intermediated by banks.^[15] Money demand equals bank deposits and is determined by firms’ demand for loans to finance investment. It is demand for money to spend, not to hold.^[16]

When Woodford (2003, chap. 5) assumes flexible prices in a closed economy with a production function that also includes capital, it is unclear whether the definition of the NRI should assume that price flexibility is a condition of past, present, and future states of the economy, or only of current and future states. There is no agreement in the profession on this matter (Amato 2005). However, the level of the capital stock differs in the two cases. When price flexibility is only a condition of current and future states of the economy, the NRI will not be independent of past nominal rigidities or of the history of monetary policy. As a result, the classical dichotomy assumed in most Woodford-style models will not strictly hold. Recently, Borio, Disyatat, and Rungcharoenkitkul (2019) argued that the interaction between monetary policy and the financial cycle generates path dependence. As a result, past monetary policy may have changed the level of the capital stock adjustment as well as the path of the NRI. To break the classical dichotomy in this type of economy, one must add a financial sector with frictions (both on the borrowing and the lending sides of agents’ balance sheets).^[17] Woodford (2003, 373) briefly discusses this point when he introduces endogenous capital stock variations in the model and seems to allow for the predetermined capital stock to be potentially affected by past policy choices. However, Woodford’s model assumes complete markets, and, as is well known, this assumption cancels history dependence with respect to idiosyncratic shocks.^[18]

In contrast, Wicksell’s discussion of the NRI and price stability is framed within his pure credit economy, which is not frictionless. Banks intermediate between savers and borrowers or investors, and banks exist because of frictions relative to the Arrow-Debreu benchmark. Because the time-varying NRI is unobservable for commercial banks, the central bank, and economic agents, in Wicksell’s framework all economic agents are prone to misperception, which engenders possible deviations of the loan market interest rate from the NRI (Trautwein 1997). As a result, the additional means of payment that are created (when the loan market rate is below the NRI) set into motion Wicksell’s cumulative process of income and price changes (discussed in section 3). While markets are not complete in Wicksell’s pure credit economy, they are complete in Woodford-style models.^[19]

The discussion so far has not done justice to a crucial aspect of Wicksell’s notion of the NRI. Wicksell’s second definition of the NRI puts the capital stock at the center of his pure credit economy—not just the level of the capital stock, but also its time structure. When banks (or a central bank with imperfect information) set the market rate of interest below the NRI, there is excess borrowing and investment by firms.^[20] In contrast to Woodford’s version of Wicksell, the divergence in Wicksell’s concept between the market interest rate and the NRI generates a saving-investment imbalance at time t leading to a sequence of future output and inflation gaps. Even in an economy with flexible prices as assumed by Wicksell, fluctuations around the NRI produce nominal as well as real effects. These effects are driven by the limited information available to capital market participants. This constitutes a major difference from Woodford’s model or most DSGE models that include financial frictions, an infinite horizon for the intertemporal optimization by the representative household, rational expectations, and a transversality condition that rules out rational bubbles, excess specific capital, and unpaid debt (Trautwein 2020). In these models, a gap between the real market interest rate and the NRI is associated with a contemporaneous output gap. Future output gaps depend only on future interest-rate gaps. Woodford-style models and DSGE models display a period-by-period equilibrium.^[21]

A few recent studies do encapsulate some Wicksellian features in an otherwise New Keynesian framework (see appendix 1 for a short presentation of the core of the New Keynesian framework). For example, Mazzocchi (2013) has a DSGE model in which price level changes are disequilibrium phenomena consistent with excess investment or savings at the “wrong” market real interest rate (i.e., different from the NRI).^[22] Closer to Wicksell’s concept of disequilibrium, Rungcharoenkitkul and Winkler (2021) extend a New Keynesian model by introducing incomplete information. The monetary authority and private agents must learn about the NRI and infer each other’s information from observed macroeconomic developments. As in Wicksell (and Mises), an informational feedback loop emerges when each agent underestimates the effect of the inferences others make from his own action. This mechanism may lead to large and persistent changes in the perceived NRI that are disconnected from fundamentals.

In summary, differences between Woodford-style models and Wicksell relate to the speed of markets’ adjustment to equilibrium and to how complete agents’ information matrix is. Woodford-style models are based on intertemporal optimization in an economy with labor (and homogeneous capital), imperfect competition, and price stickiness. While financial frictions due to asymmetric information could be added, these do not interfere with the continuous intertemporal general equilibrium. They only amplify fluctuations following shocks.^[23] Instead, Wicksell’s pure credit economy is characterized by an intertemporal coordination failure between savers and investors in the Austrian school tradition (e.g., Hayek 1935), by imperfect capital markets due to incomplete information, and by trading at “wrong” interest rates (Laidler 2011). In Wicksell’s economy, the main concern is with real disequilibrium business cycles triggered by “wrong” interest rates and driven by saving-investment imbalances.^[24] For Wicksell—as well as Keynes—price and wage flexibility would not per se eliminate the effects of “wrong” market interest rates nor induce their correction.

Appendix 2 contains a summary of the NRI in Wicksell, main differences from Mises, and the NRI in Woodford and Woodford-style models.

2.2. Wicksell’s Cumulative Process, Disagreement with Mises, and Differences with Woodford’s Economic Dynamics

In chapter 9 of Interest and Prices, Wicksell (1936) methodically describes his cumulative process. If for some reason the market rate of interest fixed by the banks is lower than the NRI, this will start Wicksell’s cumulative process of inflation, characterized by the economy adjusting to an excess of investment over savings. Wicksell’s disequilibrium is the result of a failure of the coordination mechanism in the capital market, not in the goods or labor market. If banks (or the central bank) set the market rate of interest below the NRI, demand and supply excesses in the capital market will be cleared by open market operations. Therefore, households and firms will condition their optimal plans for saving and investment on the observed market real rate of interest, although these plans will not be mutually consistent, since the real value of households’ savings will not be matched by the value of the capital stock value chosen by firms. This implies an intertemporal disequilibrium because there is no counterpart excess demand or supply in the goods market. In Wicksell’s pure credit economy, the connection between money creation and nominal income is examined in its out-of-equilibrium dynamics from one level of money and nominal income to another level of money and income.

In contrast to what may be suggested by Woodford-style models, Wicksell did not rely exclusively on static expectations to analyze the cumulative process. Strictly speaking, he used static expectations only in presenting the stationary state of his model.^[25] Wicksell was well aware that the system’s stationary state should display a constant price level, so for him the challenge was the evolution of inflation expectations over the disequilibrium cumulative process (e.g., Leijonhufvud 1981; Boianovsky and Trautwein 2004). First, Wicksell assumed that economic agents believe in a “normal” inflation rate to which the economy would tend. However, he later discussed alterations to his cumulative process in which expectations are assumed to be adaptive^[26] or even explosive.^[27] Wicksell (1936, 148) did allow nonstationary price expectations: his cumulative process can become exponential if the elasticity of price expectations is greater than unity, even if there is no divergence between the market rate of interest and the NRI. Therefore, Wicksell considered learning in his cumulative process by shifting expectations from static to adaptive and forward looking.

In addition, Wicksell’s systematic presentation of his cumulative process involves no increase in capital goods following a positive productivity shock. If real wages increase, the rise in productivity should lead to a rise in real capital, but in a 1909 essay Wicksell (1999, 2, 42) assumes that “real capital and real wages do not undergo any change.” Under these circumstances, even if prices fall, money wages must also fall, and therefore the entrepreneur will have the same return as if prices had remained constant. Essentially, Wicksell discards the possibility of capital accumulation through forced saving.^[28] This was Wicksell’s view prior to his debate with Davidson^[29] and his criticism of Mises on forced saving.^[30]

However, in a crucial concession to Mises, Wicksell admitted later that the market rate of interest and the NRI are interdependent. Wicksell then stated that forced saving could induce the real rate of interest to decrease, prolonging the upward movement of prices. He introduced the possibility of capital accumulation in part 3 of volume 1 of Lectures on Political Economy (Wicksell 1934).^[31] But he did not deal with the maladjustments that the cumulative process can generate in the capital structure or the impact such maladjustments may have on employment and income.^[32] While Wicksell originally disagreed with Davidson and Mises that the increase in productivity will result in a rise in wages and should immediately lead to an increase in real capital, it becomes clear that the sufficient condition for the cumulative process to occur is that the ex ante NRI should be capable of varying independently of the loan rate of interest (Myrdal 1939, 54ff.). The necessary condition for this to happen is the existence of some lag in the convergence of the two rates.

By building on such adjustment lag and focusing on relative price movements, Mises extended Wicksell’s cumulative process and developed his own theory of the business cycle. The fundamental differences between Wicksell and Mises are that for the latter the NRI and the market rate of interest are interdependent and a credit expansion can result in forced saving with a corresponding decline in the NRI. While the market rate of interest and the NRI could diverge due to productivity shocks à la Wicksell or due to an initial credit expansion à la Mises, the business cycle will last as long as is necessary for the two rates to converge in a new equilibrium. For Mises, banks cannot keep the loan rate of interest below the NRI for long. Attempts will result in either the NRI declining to the loan rate as real capital formation results from “real savings” or nonbank creditors raising loan rates to compensate for rising prices. If banks resist by maintaining the low loan rate, the economy will follow a disorderly unraveling toward a crisis. Wicksell’s cumulative process could end in hyperinflation or deflation, but he did not discuss the attendant disorders in production, the capital structure, employment, and the income distribution. Wicksell was clearly aware of the opposition between static and dynamic analysis in economics^[33] and explicitly admitted that he could not contribute to the latter.^[34]

2.3. Money Neutrality in the Long Run?

In his pure credit economy, Wicksell rejects the assumption of a constant velocity of money, which was instead consistent with his “pure cash” economy. In his pure credit economy, lending and borrowing occur in a competitive banking sector, and the classical dichotomy disappears: “Money is continually becoming more fluid, and the supply of money is more and more inclined to accommodate itself to the level of demand” (Wicksell 1936, 110). This is also the case in modern inflation targeting frameworks. As in Wicksell, in Woodford-style models—and in the current consensus in the profession—money is not neutral in the short run, which allows monetary policy to regulate the price level (or inflation) by controlling interest rates.^[35]

As mentioned above, Wicksell came to accept Mises’s argument that the loan rate of interest and the NRI were interdependent, but he did not consider himself capable of elaborating a theory of the business cycle. This was undertaken first by Mises and then in 1931 by Hayek (1935). Mises’s business cycle theory evolved from his Theory of Money and Credit (1934) to reach its final stage in Human Action: A Treatise on Economics (1949). It is useful to discuss the key differences between business cycle dynamics according to Mises and according to Wicksell’s cumulative process. While Mises agrees with Wicksell that the NRI is time varying, for him the NRI cannot be a barter rate and is not unique.

2.3.1. Wicksell’s Barter NRI and Mises’s Monetary “Originary Interest”

In Human Action, Mises developed the concept of “originary interest,” which is best understood by referring first to The Theory of Money and Credit, where Mises integrated monetary analysis within the Austrian theory of marginal value with the stated objective of explaining money’s purchasing power. For Mises, explaining the determination of the loan market interest rate is not formally different from explaining the determination of the ratio between money and other economic goods. In his framework, the interest on loans or the monetary rate of interest is indeed identical to the interest on capital.^[36] Changes in the exchange ratio between “present goods” (i.e., goods immediately available for consumption) and goods of “higher orders” (i.e., goods not yet ready for consumption) “are not different phenomena from the variations in the objective exchange value of money” (Mises 1981, 388). Practically, this means that an increase in the money supply, ceteris paribus, brings about excess cash balances, which implies market pressure toward raising goods prices. But Mises stresses that money does not flow into the economy uniformly and instantaneously. It first flows toward intermediate goods because of credit expansion, so that production goods prices rise more than consumption goods prices. This is tantamount to a fall in the rate of interest (Mises 1981, 388).

Similarly, the fall in the purchasing power of money mirrors the rise in the price of production goods relative to that of consumption goods. For Mises, only the existence of money makes it possible to analyze the difference in value between present and future goods. In contrast to Wicksell, Mises argues that in a barter economy the phenomenon of interest could never be isolated from the evaluation of future price movements of individual goods. Thus the NRI cannot be defined as the rate of interest that would prevail in a barter economy because such an economy would have no rate of interest. And even if there were such an NRI, it would still be irrelevant for the analysis of a monetary economy. The relevant benchmark is no longer the Wicksellian NRI that would exist in a barter economy, but rather the monetary interest rate that would exist in the absence of credit expansion (Mises 1998, 547–62).

Mises’s concept of the rate of interest changed over time. In his last major work, Human Action, he presents the phenomenon of interest as the manifestation of time preference, no longer referring to Böhm-Bawerk’s NRI. For Mises, the originary rate of interest is the discount of future goods against present goods, an expression of the category of time preference. It is the ratio of the value assigned to the satisfaction of wants in the immediate future to the value assigned to that same satisfaction in the distant future. He writes, “It is a ratio of commodity prices, not a price in itself” (Mises 1998, 523). While Wicksell’s and Woodford’s analysis of inflation is based almost entirely on changes in the general price level, Mises’s analysis is based on variations of relative prices in the time structure of capital goods.^[37]

The concept of originary interest can be related to Frank Ramsey’s (1928) classical growth model. With population growth 𝑛 and no uncertainty, r* is the general equilibrium interest rate (NRI):

$$r^{*} = \frac{1}{\varphi}\dot{c} + n + \beta.$$

The NRI moves in tandem with households’ discount rate β and the rate of population growth n, and it moves inversely to the intertemporal rate of substitution $\varphi$ weighted by growth rate of per capita consumption $\dot{c}$. In chapter 19 of Human Action, Mises argues that Wicksell’s NRI coincides with the rate of interest on loans only in the stationary state of Wicksell’s pure credit economy. In such a case, he writes, “we may call this rate the neutral rate of interest” (Mises 1998, 535). Such a neutral rate of interest exists only in the stationary state where money is neutral and coincides with households’ discount rate β (Tamborini, Mazzocchi, and Trautwein 2014).

In a growing economy, as in Woodford-style models and most DSGE models, the NRI will also be driven by other forces, notably shocks to preferences and technology. For Mises, in a growing economy the originary interest rate will additionally be driven by risk and uncertainty (e.g., credit risk, sovereign risk, geopolitical uncertainty) as well as by monetary policy. All these forces can bring lasting changes in the final originary interest rate. Therefore, in Mises’s dynamic analysis there is no single originary interest rate; there is only a tendency toward the establishment of such common rate. According to this narrative, shocks such as technological or monetary policy shocks alter not a state of equilibrium but a process which tends to equilibrium. The reason credit expansion by banks can lead the loan market monetary rate to deviate temporarily from the tendency to long-run equilibrium is the nonneutrality of money in a growing economy.

2.3.2. Mises’s Credit Cycle

For Mises, a credit expansion by banks induces the gross rate of interest on loans to decline and stimulates economic activity.^[38] No broad price effect occurs until the additional supply of money has affected the prices of goods and services. However, the decline in the gross market rate of interest on loans affects firms’ calculation about the probability of success of investment projects. The upswing starts, and provided that the credit expansion continues, the gross rate of interest on loans will tend to increase to accommodate a positive price premium. This process eventually makes it possible for the increasing market rate to catch up with the originary interest rate plus the positive price premium. For Mises, the credit cycle induces an expansion in the time dimension of the structure of production (capital) that initially puts upward pressure on intermediate and capital goods, contributing to a decline in the originary interest rate. The process continues until the fall in the originary interest rate is large enough to offset the gap (between the gross interest rate on loans and the originary interest rate) created at the start of the credit expansion. Alternatively, if banks continue the credit expansion, a hyperinflation process develops.^[39]

The credit expansion will generate additional purchasing power that can enter the economic system in different ways, and Mises noted that some relative prices will be affected earlier than others. Agents and sectors whose purchasing power rises earlier than others may face lower relative prices for the goods and services they demand than agents and sectors who demand the same goods and services but whose purchasing power only increases later. Prices and wages are affected at different times and to different extents.^[40] These relative prices changes will affect the structure of business, the size and composition of production in the various branches of industry, consumption, and wealth and income distributions.^[41] In contrast to Wicksell’s cumulative process, such changes can modify the originary interest rate and permanently alter the capital stock value and its time structure; Mises (1998, 539) writes, “In the changing economy, the rate of interest can never be neutral. In the changing economy, there is no uniform rate of originary interest; there only prevails a tendency toward the establishment of such uniformity.” Money is not neutral even in the long run.

This analysis contrasts also with Woodford-style models and more broadly with the current consensus, which holds that central banks control the nominal interest rate and, given sticky prices, affect the real rate on interest but not the NRI.^[42] According to this consensus, central banks control aggregate demand to preserve price stability, ensuing changes in investment do not affect savings, and changes in current output have no effect on potential output (Fontana 2007). The crucial assumptions of Woodford-style models and most DSGE models are that the level of savings, potential output, and NRI are independent of monetary policy; they are solely driven by technical progress, labor force growth, and the relative price of capital.^[43]

Finally, the time horizon of the real effects of monetary policy is unclear in Woodford (2003). The introductory chapter of the book and the discussion of investment in the neo-Wicksellian model (361–72) suggest that money is nonneutral also in the long run, as pointed out by Boianovsky and Trautwein (2006). However, Woodford rarely discusses monetary policy nonneutrality. This may be because in his framework nonneutrality is defined as the discrepancy between the flexible-price benchmark of a natural rate of output and actual output under nominal rigidities, an admittedly minimalist concept of monetary policy nonneutrality. Clearly, monetary policy nonneutrality in the long run leaves numerous and fundamental questions unanswered, but discussing them is beyond the scope of this article.

3. Estimate of the US NRI Based on Wicksell and Mises

Following the theoretical discussion above, this section uses the US national income and product accounts to compute the NRI as suggested by the work of Wicksell and Mises. As proposed by Wicksell and further elaborated by Mises (1998, 487–514), capital formation is imputable (in the long run) to land, labor, and time. For these authors, capital (in contrast to capital goods) is not an independent factor of production that earns a net rent for its owner. Instead, capitalist-entrepreneurs are remunerated for the risk they take on in advancing liquidity to the other factors of production; this is the monetary expression of Wicksell’s free and mobile capital, which is necessary as means for sustaining those who furnish the labor and land during the time required for the production of fixed real capital. Businesses’ real return on investment^[44] is calculated by summing the net operating surplus of nonfinancial corporations and deducting all advances to factor owners which are not directly linked to interest on financial capital (such as “rental income” and “proprietors’ income”), which include a significant wage component from sole proprietorships and partnerships, and the often unimportant “other transfer payments.”^[45] Wicksell’s NRI, the businesses’ real rate of return on investment, is therefore obtained by summing “corporate profits adjusted for inventory valuation and capital consumption of domestic companies” and “net interest paid on financial assets” (i.e., the numerator) and then dividing it by the net stock of produced assets (private and nonresidential) augmented by capitalists’ expenditure on factor incomes, labor, and land (i.e., the denominator).

As shown in figure 4, the NRI of the US oscillated between about 5.8 percent and 7.8 percent from 1980 to 2020. The average was 6.8 percent over 1980 and 2020, declining slightly to 6.3 percent in the post-2008 period.^[46] This decline, probably the outcome of accommodative monetary policies,^[47] pales in comparison to the trend decline in the sample period 1999–2020 documented in, for example, Brand, Bielecki, and Penalver (2018) and Caballero, Farhi, and Gourinchas (2017). In figure 4, the NRI does not approach zero and remains well above the federal funds rate.

Figure 4.The US NRI (percent), the fed funds rate (right-hand scale), the risk premium, and the VIX

Sources: Jordà, Schularick, and Taylor (2017); Chen et al. (2022); and author’s calculations.
Note: VIX is available beginning in 1990. VIX is the ticker symbol and the name for the Chicago Board Options Exchange’s CBOE Volatility Index, a widely used measure of the stock market’s expectation of volatility based on S&P 500 index options.

In the stationary state,^[48] the Misesian originary interest rate would be consistent with a quarterly discount factor of 0.983 on average (i.e., an average NRI between 7.0 percent and 6.5 percent). These rates would also be consistent with Caballero, Farhi, and Gourinchas’s (2017) estimates of the return on US physical capital. However, these NRI estimates do not properly distinguish the NRI from Mises’s uncertain profit rate in a growing economy.^[49] So, short of modelling such risk, an approximation of the equity risk premium from Jordà, Schularick, and Taylor (2017) and Chen et al. (2022) may be computed as the gap between risky and safe assets (nominal). This measure of risk rose from about 2.4 percent in the period 1980–2008 to 8.0 percent in the period 2009–20, which is similar to estimates in Caballero, Farhi, and Gourinchas (2017).

3.1. What about the Wedge between Real Returns on Bonds and the Real Return on Physical Capital?

As discussed in section 1, the DSGE models used to estimate the NRI identify a “risk premium shock” as the main driver of the decline in the NRI. Using Fisher (2015), the so-called risk premium shock can be interpreted as a shock to demand for safe and liquid assets. However, Fisher (2015, 514) himself suggests relabeling the so-called risk premium shock as a “safety and liquidity premium,” a “liquidity preference,” or a “money demand” shock. Fisher warns that this structural interpretation of the shock is possible only for certain values of an exogenous stationary disturbance term affecting the demand for liquid assets. Under other circumstances, however, there can be a serious mismeasurement of the liquidity demand shock in the Smets-Wouters model (2007), on which Neri and Gerali (2019) based their own model. In addition, as argued by Fisher (2015), in such circumstances, the first-order condition for risk-free bonds will lack a variable that represents the supply of safe and liquid assets, a point also forcefully made in Borio, Disyatat, and Rungcharoenkitkul (2019).^[50] Therefore, when the decline in the NRI is attributed to the so-called risk premium shock of Neri and Gerali (2019) or the “capital risk” of Caballero, Farhi, and Gourinchas (2017), these may not be based on structural parameter values that provide a narrative consistent with widely accepted measures of risk premium and volatility. Appendix 3 displays the behavior of US house prices and the S&P 500 cyclically adjusted price-to-earnings ratio, often used as a proxy to forecast returns. Despite the decline in the time series around 2008–9, they display an upward trend which is inconsistent with a narrative suggesting that there is a low demand to hold risky assets. Instead, the upward trend is more consistent with, for example, Thomas Mayer and Gunther Schnabl’s (2021) narrative of a “monetary overhang” since the mid-1980s that accelerated since the end of the 1990s and lifted financial asset prices on the back of low interest rates. In the Gordon model (Gordon and Shapiro 1956) used also by Caballero, Farhi, and Gourinchas (2017), equity dividends are discounted by the difference between the real interest rate and the dividend growth rate. As monetary policy lowered the real interest rate and dividend growth increased, so did equity prices.

An additional technical consideration is that DSGE models used to estimate the NRI may require household utility functions that are not time separable—that is, utility functions in which risk aversion is not simply the opposite of the elasticity of intertemporal substitution. The two parameters have been estimated in the literature (see Outreville 2014 for a survey of risk aversion estimates and Thimme 2017 for the elasticity of intertemporal substitution). Results vary significantly across studies. Risk aversion estimates range from 55 percent in Mehra and Prescott (1985) to 0–10 percent in Haliassos and Hassapis (2001). Estimates of the elasticity of intertemporal substitution vary from 0.05–2.00 in Hung (1994) to 0.01–0.06 in Chapman (2002). Given the wide range of estimates for these deep parameters, DSGE evidence on the drivers of the decline in the NRI is to be taken with caution, in particular because the models in figure 2 use time-separable functions. To illustrate this fundamental point, using option prices and an Epstein-Zin utility function (Epstein and Zin 1989); Blackburn (2008) finds that the risk-free rate is affected positively by risk aversion and negatively by the elasticity of intertemporal substitution. However, Blackburn finds, risk aversion mostly affects the risk premium. It is the elasticity of intertemporal substitution—and not risk aversion—that affects volatility negatively. These results confirm Kandel and Stambaugh’s (1991) theoretical model.^[51]

Since the ratio of the equity risk premium to the risk-free rate increased from about 1 percent to about 2 percent in 2008, the enduring fall in the NRI estimated using semistructural and DSGE models may result from a rise in the elasticity of intertemporal substitution. This increase may explain the fall in volatility observed in the VIX from 2008 at least until 2017, the end of the sample period used by many estimates (e.g., Caballero, Farhi, and Gourinchas 2017). In addition, the increase in the elasticity of intertemporal substitution may be the main driver for the decline in the estimated real rates of interest (real yields). These arguments reinforce the view that monetary policy may affect the NRI as suggested by the writings of Mises as well as Borio, Disyatat, and Rungcharoenkitkul (2017) and other observers in the tradition of Wicksell.

4. The Transmission of US Monetary Policy and Returns on Assets

This section explores the hypothesis that monetary policy may have played an important role in increasing the wedge between the return on safe assets and the return on physical capital. To that end, it uses Korobilis’s (2013) time-varying parameter dynamic factor model to study the domestic and international transmission of US monetary policy shocks using a large set of macroeconomic variables, notably those included in the discussion about the possible explanation for the gap between the real return on physical capital and returns on financial assets. As Korobilis’s model is well known, and to conserve space, it is not described.

4.1. Data and Data Treatment

The database is from Jordà, Schularick, and Taylor (2017); Chen et al. (2022); and Jordà et al. (2019). The sample period includes annual data from the last four decades (i.e., 1980–2020), during which estimates of the NRI show a declining trend. According to Borio, Disyatat, and Rungcharoenkitkul (2017), this is the only period when the stability in the link between real interest rates and saving-investment determinants that is always assumed in models that estimate the NRI has existed.^[52] Data availability justifies the selection of fifteen out of the eighteen countries in the database: Australia, Belgium, Denmark, Finland, France, Germany, Italy, Japan, the Netherlands, Norway, Spain, Sweden, Switzerland, the United Kingdom, and the United States.

All nominal variables are deflated by the corresponding consumer price indices. Variables expressed in percent and in ratios to gross domestic product (GDP) are not modified. All asset rates of return are defined in and Jordà et al. (2019) and briefly presented in appendix 4. The risk premium is computed as the difference between the returns on risky and safe assets from and Jordà et al. (2019). In addition, real rates of interest for three-month, one-year and ten-year US government bonds are from FRED, the database maintained by the Federal Reserve Bank of St. Louis. Real effective exchange rates are from the International Financial Statistics dataset of the International Monetary Fund. Following Mayer and Schnabl (2021), the marginal productivity of real capital is proxied by the change in real GDP relative to the previous year divided by the real investment of the current year, and monetary overhang is defined as the increase of accumulated M1 relative to accumulated nominal GDP with year 1980 = 100. The ratios of the US nondurable and durable consumption to investment goods prices, of nondurable and durable consumption to intermediate goods prices, and of intermediate to investment goods prices are from the Organisation for Economic Co-operation and Development Producer Prices by Production Type database. The NRI time series is the estimate discussed in section 3.

Finally, following the insight—not the methodology—of Miranda-Agrippino and Rey (2020), the common components of the time series of all countries (except the US) are computed using the Forni et al. (2005) one-sided generalized dynamic factor model (GDFM).^[53] These common components encapsulate the global forces driving the fourteen-country time series. These time series are the common components of real GDP, Consumer Price Index (CPI) inflation, short- and long-term interest rates, general government revenue and expenditure, general government debt-to-GDP ratios, private domestic credit, total equity return, total government bonds return, total housing return, equity capital gain, government bonds capital gain, housing capital gain, equity dividend return, bonds coupon return, housing rent return, capital or wealth return, risky assets return, safe assets return, banks’ capital ratio (leverage), banks’ loan-to-deposit ratio, and banks’ noncore funding ratio. The policy rate is the Wu-Xia shadow rate (Wu and Xia 2016), which is justified by the main focus of this section—that is, to explore the domestic and global effects of US monetary policy independently of whether it takes a conventional or unconventional form. Appendix 5 contains the list of the eighty-nine time series used in the estimation.

Time-series nonstationarity is eliminated using the ideal band-pass filter (Corbae and Ouliaris 2006) masking periodicities longer than sixteen years, which allows the analysis of business cycles—periodicities between two and eight years—and the financial cycle.^[54] This approach avoids ad hoc decisions given the frequent conflicting results for pretests for the degree of integration and, crucially, avoids first-differencing, which is a high-pass filter with a gain function “that deviates substantially from the squared gain function of an ideal high-pass filter” (Koopmans 1974).^[55]

Several statistical tests are run to determine the number of factors for the model estimation. Stock and Watson’s (2005), Bai and Ng’s (2007), and Onatski’s (2009) procedures suggest two dynamic factors, while Hallin and Liška’s (2007) ${IC}_{1}$ procedure suggests one to three dynamic factors. Therefore, two factors are chosen for the estimation. The Bayesian information criterion suggests one lag with two static factors.^[56]

4.2. Estimation and Results

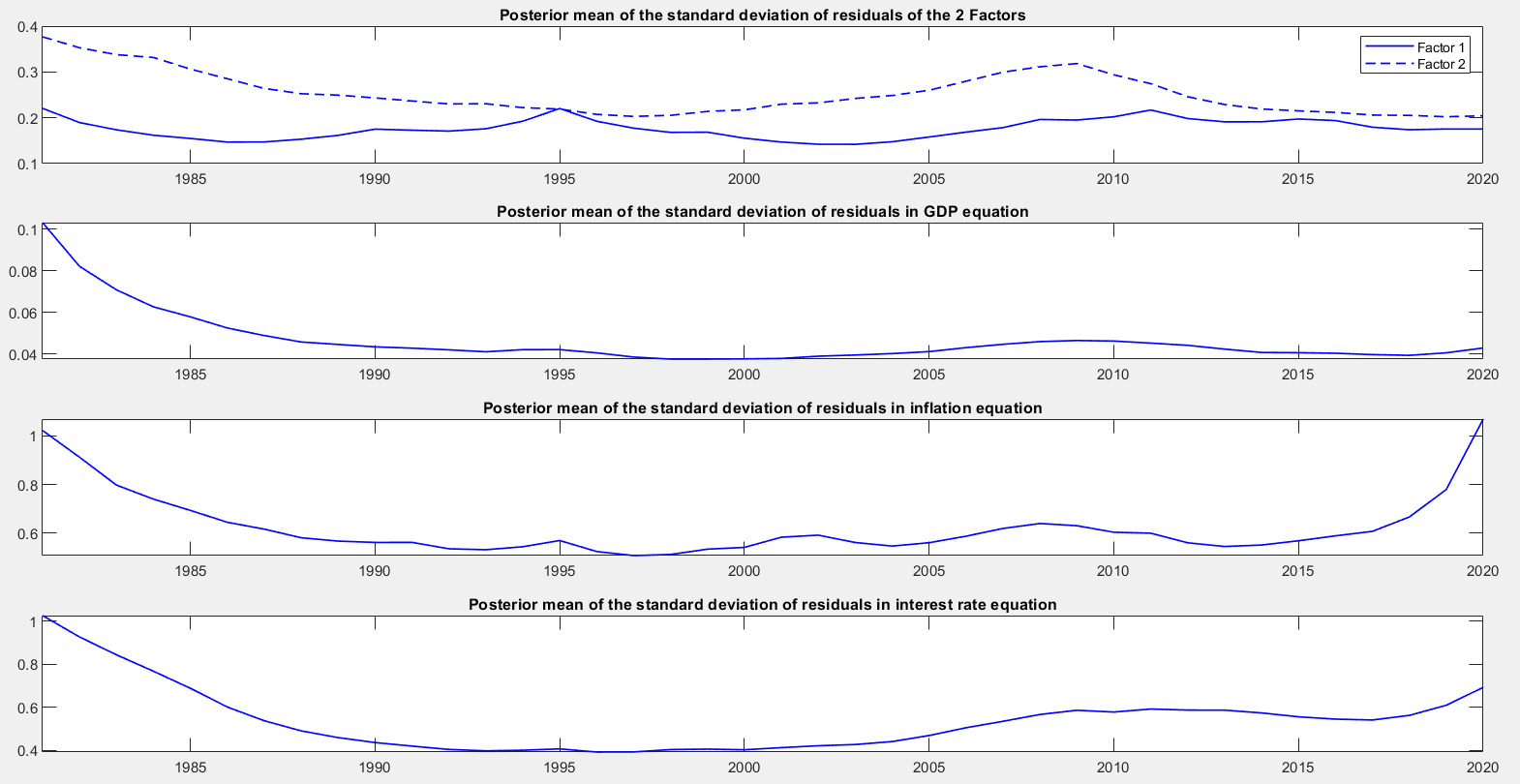
Given possible changes in the data-generating process, the time-varying parameter dynamic factor model of Korobilis (2013) is estimated. It allows the investigation of both the potential instability in the coefficients of the VAR and stochastic volatility (as in Primiceri 2005) possibly linked to the GFC and the COVID-19 pandemic. As recently argued by Schlaak, Rieth, and Podstawsky (2023), using both a valid instrument and heteroskedasticity to estimate monetary policy shocks sharpens structural inference, leading to larger effects on production and prices than monetary shocks identified via an instrument only. Given the limited sample length, no training sample is used. Noninformative priors are used for the VAR equation with one lag. The hyperparameter priors are K(Q) = 0.001, K(S) = 0.1, and K(W) = 0.5, where Q denotes shocks to the VAR and S denotes shocks to the systematic part of monetary policy (i.e., shocks that are correlated within each equation). The value for Q is tighter than the one used by Giorgio Primiceri (2005): 0.5 as opposed to 0.01; and the value for S is the same: 0.1.^[57] Shocks represented by W are potentially correlated across equations and could therefore affect the monetary policy equation. The main result is that the data provide no evidence of a significant change in the parameters of the model or those determining the distribution of shocks affecting the policy response to inflation and output.

The use of a tighter parameter for Q suggests that accounting for multivariate stochastic volatility is important for capturing possible heteroskedasticity and nonlinearities. This is not surprising given that the sample comprises two major shocks: the GFC and the COVID-19 pandemic. Indeed, figure 5 shows that there are no significant changes in volatility over time except for in the interest rate residuals following the GFC and around the pandemic (bottom graph). The same pattern appears for the inflation equation (third graph), which also shows the weakness in the economy of the United States in 1995 and 2002.

Figure 5.US stochastic volatility estimates

Note: Time-varying standard deviations of residuals in the time-varying parameters FAVAR model.

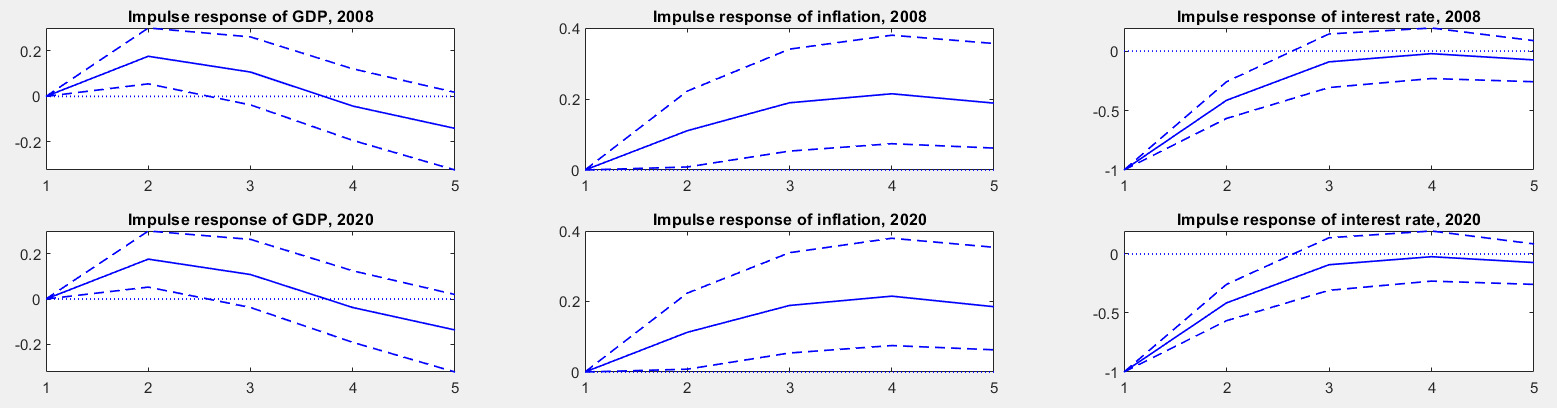
The estimated responses of US monetary policy shocks on US output and inflation for 2008 and 2020 do not differ (figure 6). In both periods, following a one-standard-deviation reduction of the policy rate, real GDP increases during the first year, with the expansion lasting for three years. Inflation increases during the second year and is more persistent. These results broadly match accepted results in the literature (e.g., B. S. Bernanke 2020; Dou et al. 2020).

Figure 6.Impulse responses of the effects of US monetary policy shocks on domestic output and inflation, 2008 and 2020

Note: IRFs display the median response and its 16th and 84th percentile confidence intervals over five years.

All variables are standardized, which facilitates comparability across shocks. All impulse response functions (IRFs) in figure 6 display the median response and its 16th and 84th percentile confidence intervals over five years—the standard length in empirical analysis. Results for US real and nominal variables as well as for global variables accord well with the methodical analysis of the domestic and global dimensions of US monetary policy in Obstfeld (2020) (figure 7).

Figure 7.Impulse responses of the domestic and international effects of US monetary policy shocks, 2008 and 2020

Note: IRFs display the median response and its 16th and 84th percentile confidence intervals over five years. Global variables are the common component of the time series of all countries (except the US) and are computed using the Forni et al. (2005) one-sided GDFM. The estimated responses of US monetary policy shocks on US output and inflation for 2008 and 2020 do not differ.

As shown in figure 7, the accommodative US monetary policy shock lowers both ends of the yield curve, but especially the long end. The monetary policy shock leads to a decline in real interest rates on government bonds at all maturities available in the dataset, but especially at maturities of one and ten years. Domestic private credit to households and nonfinancial corporations increases.^[58] Banks experience an expansion in liquidity as their loan-to-deposit ratios decline (the money stock rises) and consistently reduce their recourse to noncore funding sources. There is evidence of a “liquidity preference” shock à la Fisher (2015) as (real) money increases for about two and a half years, and (real) narrow money displays a persistent, albeit small, rise after a short-term decline. Accordingly, the monetary overhang measure remains positive throughout. Banks’ capital ratio drops as a result of banks’ increase in leverage. Real house prices rise over about one and a half years. The current account balance displays a deficit in the short term, and the real effective exchange rate appreciates. These last results accord well with the Obstfeld and Rogoff (1995) model, in which a large economy such as the US experiences a real effective exchange rate appreciation following a decline in their policy rate, which generates a global positive output effect (via the expenditure-switching channel of monetary policy).

In addition, the IRFs in figure 7 show that the accommodative monetary policy shock produces a decrease in total return on equity and a persistent decline in total return on government bonds. The decrease in total return on equity is not entirely compensated by the highly persistent capital gains, while the dividend yield displays a small reduction.^[59] The decline in the total return on government bonds is driven by a persistent and material negative capital loss and a smaller coupon return. Total return on wealth shows a persistent increase. Finally, the accommodative monetary policy shock reduces the return not only on safe assets but also on risky assets, so that the risk premium—the difference between returns on risky and safe assets—declines over about two and a half years. These results are consistent with the hypothesis that accommodative monetary policy has a lasting effect, raising the return on equity relative to that on government bonds via a significant increase in capital gains that more than offsets a small decline in the dividend yield. The decline in the dividend yield matches the decline in the profit rate well.

The IRF of the NRI displayed in figure 7 increases during the first two years and follows a pattern that is similar to the pattern of the marginal productivity of capital (it becomes insignificant after two years).^[60] Clearly, the NRI is an aggregate measure for the US. However, according to Mises’s originary interest concept and his theory of the business cycle, changes in the NRI need to be linked to changes over time in the relative producer prices of goods at different stages of production. The pattern of relative price changes is captured by the IRFs of five relative prices: the relative prices of durable and nondurable consumption goods compared to intermediate and investment goods, as well as the relative price of intermediate compared to investment goods.^[61] Specifically, the price of intermediate goods increases relative to that of durable consumption goods for one and a half years, and the price of investment goods increases relative to that of nondurable consumption goods for two and a half years. These two relative price increases could be interpreted as a decline in Mises’s originary interest rate. There is also a rise in the price of durable consumption goods relative to that of investment goods for one and a half years and a rise in the price of intermediate goods relative to that of investment goods for two years. These two relative price changes suggest an increase in Mises’s originary interest rate. However, the net effect of all relative price changes is a clear decline in Mises’s originary interest rate (NRI), as the relative price changes that reduce it are 15 percent larger and last longer than the relative price changes that increase it.^[62]

As discussed in section 2.3.2, these opposing forces echo Mises’s view that there may be no uniform NRI and that one must consider the time structure of capital and not just the time-varying value of the capital stock. Furthermore, the pattern of relative price changes is reminiscent of the Austrian view that more roundabout methods of production imply a higher marginal productivity of capital. In fact, as stated in Mises’s business cycle theory, intermediate goods prices rise first and more than durable consumption goods prices; investment goods prices increase more than nondurable goods prices and the increase is more persistent (Mises 1998, 554–58). In addition, intermediate and durable goods prices rise relative to investment goods prices, a characteristic that seems a stylized feature of the data as reported by Karabarbounis and Neiman (2014).^[63] Overall, these results are consistent with Mises’s suggestion (finally accepted by Wicksell) that following the monetary policy shock there is likely to be a short period of “forced saving” which accompanies the expansion of the production process until the necessary consumption goods are available (i.e., before real savings increase).

Regarding the international transmission of US monetary policy, both global real GDP and global CPI rise (figure 7). Short- and long-term global interest rates drop, and global private credit increases persistently. The response of global asset returns is also similar to that of domestic asset returns. These findings agree with research suggesting the existence of a global financial cycle led by the US (e.g., Nadal De Simone and Tongzon 1997; Rey 2013; Dées and Galesi 2019; Miranda-Aggripino and Rey 2020).

Overall, the IRFs support the hypothesis that the wedge between low real yields on US treasuries and the quite stable real return on physical capital is largely attributable to persistently accommodative monetary policy. This does not necessarily exclude the possible contribution from the decline in labor share discussed by Caballero, Farhi, and Gourinchas (2017), but it is inconsistent with their conclusion of an increase in capital risk premia. The results also seem to support Mises’s theory of relative price changes during the business cycle.

5. Concluding Remarks and Implications

Recent NRI estimates derived from semistructural, structural, and DSGE models (Brand, Bielecki, and Penalver 2018) based on the investment-saving curve, the Phillips curve, and a monetary policy equation assume that investment equals savings in every period, that monetary policy does not affect the NRI, that investment misallocations do not disturb potential output or savings, and that money, even though endogenous as in Wicksell’s pure credit economy, is neutral in the long run. With no persistent saving-investment imbalances, a positive gap between Wicksell’s NRI—not Woodford’s interpretation of Wicksell’s NRI—and the loan market interest rate is excluded by assumption, and the capital market may be decoupled from the real economy.

However, if saving is not equal to investment, this may explain the positive gap between the return on securities and the return on physical real capital. Interpreting Wicksell’s NRI in a manner consistent with his writings, considering the outcome of Wicksell’s disagreement with Mises, and considering the latter’s business cycle theory all lead to a plausible explanation of the observed wedge between asset price returns and the return on real capital. Capital formation through forced saving, together with Mises’s dynamic analysis of the business cycle, provide a consistent narrative to possibly explain the discrepancy between the NRI and yields. They also explain how monetary policy could affect the NRI through the time-varying and uneven impact that a credit expansion may have on the distribution of income and wealth.

If monetary policy has lowered the NRI (Mises’s concept of the NRI), it may have perpetuated low real rates, as suggested by Borio, Disyatat, and Rungcharoenkitkul (2017, 2019), Levrero (2021), Mayer and Schnabl (2021) and others. Low and negative policy rates together with quantitative easing since 2009, especially intermediated by banks, may have exacerbated the downward pressure on the NRI by reducing returns on US government bonds, and increasing equity capital gains, two of the three stylized features identified by Caballero, Farhi, and Gourinchas (2017). At the same time, these policies may have delayed the adjustment process required for real yields and the NRI to converge on a new equilibrium.

Woodford-style models are not adequate to represent Wicksell’s NRI concept or to consider the possibility that monetary policy may affect the NRI. Using these models to guide monetary policy may lead to a stance that is inconsistent with price stability. Both these models’ neglect of the possibility that monetary policy could persistently alter the time dimension of the capital stock, leading to investment misallocation, and their assumption of complete financial markets make them unsatisfactory for addressing concerns stemming from the interaction of the financial sector and the real economy. In particular, Woodford-style models are inadequate to address the interaction between financial stability and price stability.^[64]

All these concerns require useful and not just elegant models. As this article suggests, such models need to include the financial sector explicitly and to recognize that financial markets need not be complete. Moreover, the probability of default should be able to diverge from zero under certain states of the economy; “excessive” maturity transformation must be a distinct possibility; and the interplay between leverage and asset prices should be relevant not just for the value of firms, but also for the transmission of monetary policy. Inefficient equilibria could occur in these settings, which would justify policy intervention with potential welfare-enhancing effects.

If Woodford (2003) had the undesirable result of misrepresenting Wicksell’s views on the NRI and throwing confusion into the areas discussed in this article, it also returned attention to the profound work of Wicksell and the comprehensive analysis of Mises, perhaps leading the profession to revisit paradigms such as the long-run neutrality of money and the Cambridge capital controversy. Such positive outcomes could improve current economic models.